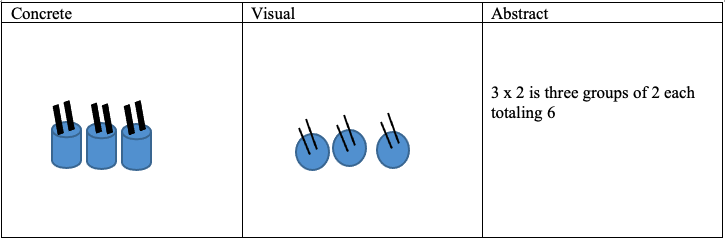
Many students fail to grasp the concept and procedural facility of multiple step mathematics approach. Since mathematics builds unto itself, as math becomes more complex, students with gaps in their learning have a uniquely difficulty time succeeding.
The concrete to visual to abstract sequence of instruction (CVA) has demonstrated effectiveness helping students who struggle with mathematics build understanding and procedural memory of mathematics processes. CVA is a graduated sequence of instruction that begins with the manipulation of concrete materials followed by use of visuals or pictorial representations and ending with problem solving with abstract notation. Importantly, during each stage, the same mathematics process and approach are supported. While CVA is helpful in establishing understanding and procedural memory, it is ineffective at helping students build fast recall of computation.
Teachers must
- Plan the abstract steps to solve a mathematics problem with each step tied to verbal reasoning (i.e. understanding of the math framed in words),
- Select or develop a manipulative that accurately relays the steps and encourages verbal reasoning,
- Teach the concrete lesson using easier to manipulate numbers until the student(s) shows accuracy with verbal reasoning at least once,
- Teach the visual lesson using more complex numbers until the student(s) shows mastery with verbal reasoning several times,
- Teach the abstract lesson using an array of complexities until the student(s) shows mastery with verbal reasoning until mastery.
Adapted from Witzel, Riccomini, & Schneider, 2008
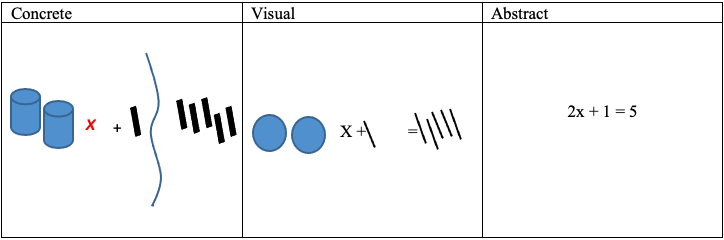
- Often students have difficulty transitioning from one stage of CVA to the next. To help students transition, use consistent language across stages and link C and V representations to the A approach.
- Students may find early success with the C stage and not want to move on.To help, use concrete objects expeditiously so that they learn the approach but do not get stuck in this stage.
- Teachers may have a hard time finding a manipulative object that accurately represents the concept. This is a normal concern since some concepts, particularly secondary level concepts, are difficult to represent concretely. Do not force the C step when inappropriate. Instead, look for a graphic organizer and attempt a Visual-Abstract approach.
Students learn the approach through CVA but do not develop fluency. This approach is designed to build understanding and memory. To establish fluency, additional approaches should be considered.
Bouck, E. C., Satsangi, R., & Park, J. (2018). The concrete-representational-abstract approach for students with learning disabilities: An evidence-based practice synthesis. Remedial and Special Education, 39(4), 211-228.
Flores, M. M., Hinton, V. M., & Meyer, J. M. (2020). Teaching fraction concepts using the concrete-representational-abstract sequence. Remedial and Special Education, 41(3), 165-175.
Morano, S., Flores, M. M., Hinton, V., & Meyer, J. (2020). A comparison of concrete-representational-abstract and concrete-representational-abstract-integrated fraction interventions for students with disabilities. Exceptionalities, 28(2), 77-91.
Linked Resources:
Florida CPALMS
http://fcit.usf.edu/mathvids/strategies/cra.html
https://www.didax.com/math/virtual-manipulatives.html
Level of Evidence:
Validated.
Many research meta-analyses tout the potential impact of CVA. For more information or insight into the history of CVA, it is important to review the alternate names of this approach:
Concrete-semiconcrete-abstract sequence of instruction (CSA)
Concrete-representational-abstract sequence of instruction (CRA)
Concrete-representational-abstract-integrated sequence of instruction (CRA-I)
Position Papers or Practitioner Publications on the Topic:
Florida Department of Education
